Moment area method
Method for finding deflections in a framed structure by the use of moment area curve.
First Theorem
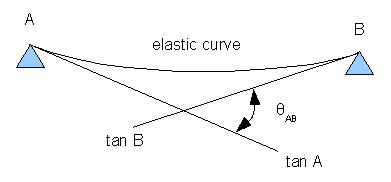
Theorem 1: The change in slope between any two points on the elastic curve equals the area of the M/EI diagram between these two points.
\[\theta_{AB} = {\int_A}^B \frac{M}{EI}\;dx\]
where
- M moment
- EI flexural rigidity
- \(\theta_{AB}\) ... change in slope between points A and B
- A, B ... points on the elastic curve
Second Theorem
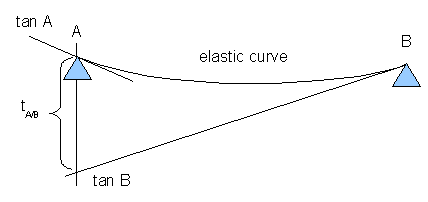Theorem 2: The deviation of the tangent at point B on the elastic curve with respect to the tangent at point A equals the "moment" of the M/EI diagram between points A and B computed about point A (the point on the elastic curve), where the deviation \(t_{A/B}\) is to be determined.
\[t_{A/B} = {\int_A}^B \frac{M}{EI} \bar{x} \;dx\]
where
- M moment
- EI flexural rigidity
- \(t_{A/B}\) ... deviation of tangent at point B with respect to the tangent at point A
- \(\bar{x}\) ... centroid of M/EI diagram measured horizontally from point A
- A, B ... points on the elastic curve
References
- Russel C. Hibbeler: Structural Analysis, 3rd Edition, Prentice Hall, 1995, chapter 8, p. 354-569, ISBN 0-02-354041-9
Links
Topic category: